Model Scaling

今天看的这篇文章还是物体识别的，链接如下：

paper: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

通常情况下，卷积网络都是基于固定的资源，然后放大(Scale Up)以提高准确率，而本文综合地分析了模型的放大(Scaling)，发现如果能调整好网络深度，宽度和资源之间的平衡，网络能有更好的效果，所有本文提出了一个新的放大(Scaling)手段，通过使用一个简单有效的混合参数，均匀地放大所有尺度的信息。

Introduction

现有的方法里面有考虑放大Resnet的，但是放大ConvNets的还没有很好的方法，最常用的是放大它的深度和宽度，也有通过图像分辨率来放大的，但是都只是通过这三个维度之一来放大，就算能同时放大三个维度，但是任意的放大只会导致不那么好的效果。

本文首先根据经验探讨，之后发现这其中的平衡是可以简单地通过使用固定的比值放大它们来实现，基于这个观察结果，本文提出了Compound Scaling Method来实现，比如如果使用$2^{N}$倍的计算资源，就简单地提高$\alpha^{N}$深度，$\beta^{N}$宽度，以及$\gamma^{N}$的图像大小，其中$\alpha, \beta, \gamma$是固定的系数，与传统的网络的比较如下：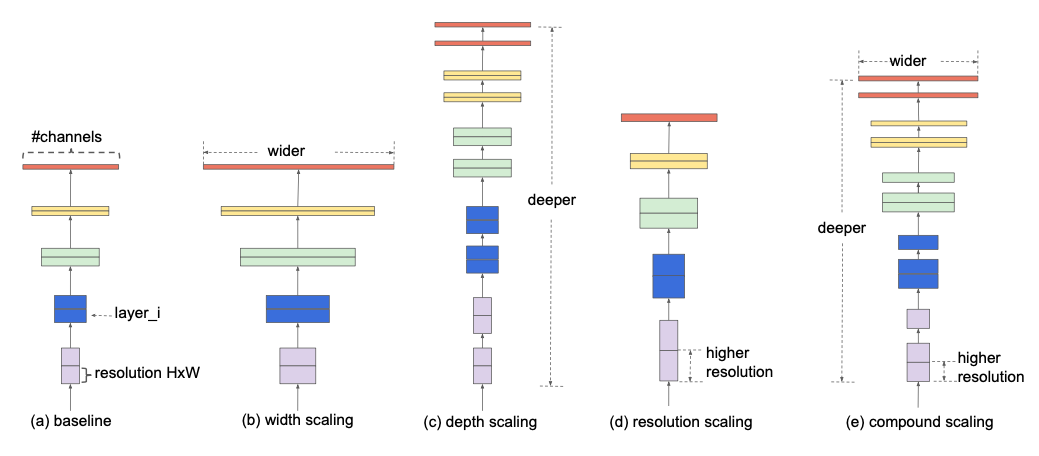

Compound Model Scaling

如果一个网络层可以定义为：$Y_{i}=\mathcal{F}_{i}\left(X_{i}\right)$，其中Tensor可表示为：$\left\langle H_{i}, W_{i}, C_{i}\right\rangle^{1}$，因此可以定义一个ConvNet为：

$$\mathcal{N}=\bigoplus_{i=1 \ldots s} \mathcal{F}_{i}^{L_{i}}\left(X_{\left\langle H_{i}, W_{i}, C_{i}\right\rangle}\right)$$

与普遍的ConvNet设计：旨在找到最好的单层结构不同，模型放大旨在不改变Baseline里预设的单层结构的前提下，拓展网络的长度，宽度或者解析度，通过固定$\mathcal{F}_{i}$，模型的设计就简单许多了，但是对于$L_{i}, C_{i}, H_{i}, W_{i}$的设计仍然有很高的自由度，所以为了进一步减小设计空间，本文限制所有的层都必须用固定的比值同步放大，所以目标可写成：$\begin{array}{rl}{\max _{d, w, r}} & {\operatorname{Accuracy}(\mathcal{N}(d, w, r))} \\ {\text {s.t.}} & {\mathcal{N}(d, w, r)=\bigoplus_{i=1 \ldots s} \hat{\mathcal{F}}_{i}^{d \cdot \hat{L}_{i}}\left(X_{\left\langle r \cdot \hat{H}_{i}, r \cdot \hat{W}_{i}, w \cdot \hat{C}_{i}\right\rangle}\right)} \\ {} & {\text { Memory }(\mathcal{N}) \leq \text { target memory }} \\ {} & {\text { FLOPS }(\mathcal{N}) \leq \text { target flops }}\end{array}$

Scaling Dimensions

对上式的问题，主要的难度就是最优化的$d, w, r$彼此影响，并且其结果在不同的资源限制下也不同，所以传统办法主要用以下维度之一来放大ConvNets：

Depth：这是最常用的放大方法，因为更深的网络往往能捕捉更加丰富，更加复杂的特征，但是更深的网络由于梯度消失问题，往往更难训练，虽然可以用跳连(Skip Connection)缓解，但在很深的网络上还是会有准确度减少的效果，结果如下中间所示：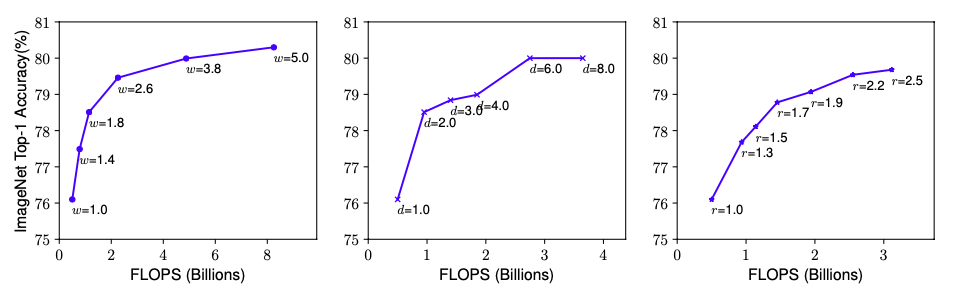

Width：放大网络的宽度对于小的模型使用的比较频繁，而实验表明，宽的网络更能捕捉细颗粒度的特征，且更易于训练，但是过宽且浅(Shallow)的网络却不能捕捉更高维度的信息，如上图左所示。

Resolution：输入的图像的分辨率提高的时候，ConvNets能捕捉更加细颗粒度的模式，但是同样的，由以上的网络(右)可以发现过高分辨率的准确率也还是会降低。

综上，只放大任意维度的网络能提高精度，但是对于更大的模型，准确率还是会降低。

Compound Scaling

由上可知，不同的维度并不是独立的，更加地，对于高解析度图片，应该也增加网络深度，比如用更加的感受野能帮助捕捉相似的但又更多像素的图片，同样的，增加解析度的同时也应该增加网络宽度，由此做的实验结果如下：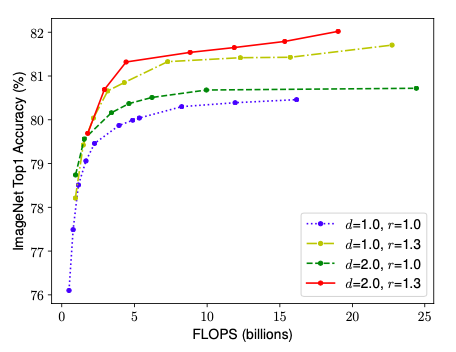

所以为了更好的准确率和效率，应该平衡好网络的各个维度。故本文使用了一种混合系数$\phi$来用以下方法同时放大以上三个维度：$\begin{aligned} \text { depth: } d &=\alpha^{\phi} \\ \text { width: } w &=\beta^{\phi} \\ \text { resolution: } r &=\gamma^{\phi} \\ \text { s.t. } \alpha & \cdot \beta^{2} \cdot \gamma^{2} \approx 2 \\ \alpha & \geq 1, \beta \geq 1, \gamma \geq 1 \end{aligned}$
其中$\alpha, \beta, \gamma$是固定的系数，且满足一定的互相限制的关系，并且$\phi$由使用者指定，并能控制，用多少资源来放大模型。

EfficientNet Architecture

既然放大模型不改变Baseline的$\hat{\mathcal{F}}_{i}$，所以一个好的Baseline很重要，本文就根据这个提出了一个新的自动调整大小的Baseline，叫EfficientNet。

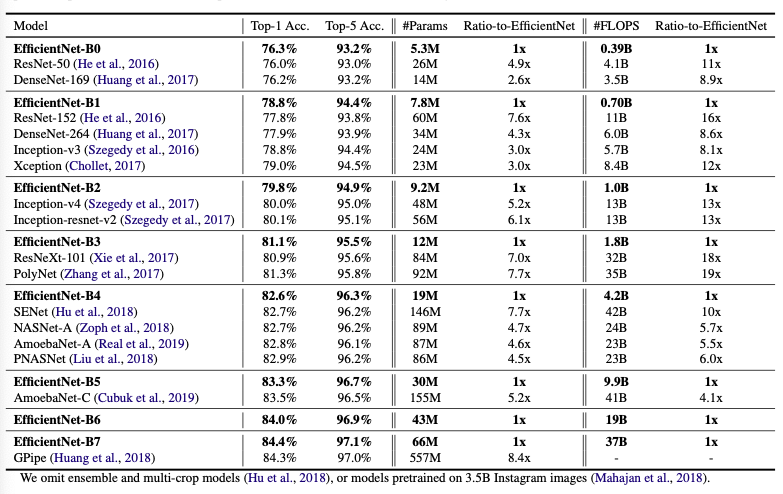
本文提出了使用$A C C(m) \times[F L O P S(m) / T]^{w}$作为优化目标，且$w=-0.07$为控制准确率和FLOPS之间的权衡的超参数，使用EfficientNet-B0作为Baseline，结果如下：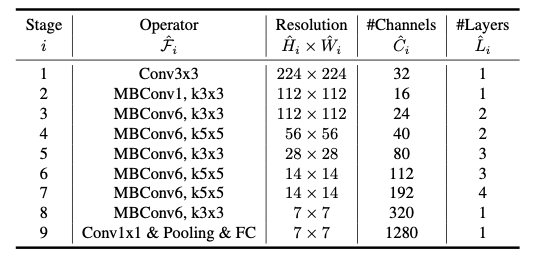

而由这个baseline开始，使用混合放大方法来放大网络，步骤如下：

STEP 1: 首先固定$\phi$，并假设两倍的资源是可用的，并给予以上两个方程做一个关于$\alpha, \beta, \gamma$的网格搜索，最后发现在$\alpha \cdot \beta^{2} \cdot \gamma^{2} \approx 2$的限制下，$\alpha = 1.2, \beta = 1.1, \gamma = 1.15$是最优解
再固定$\alpha, \beta, \gamma$，并且基于最后一个方程，使用不同的$\phi$来得到EfficientNet-B1 to B7，结果如下：